In the first three parts of this series I covered different aspects of our Reverse Engineering Intermediate Language REIL. First, I gave a short overview of REIL and what we are trying to achieve with it. Then, I talked about the REIL language itself. Finally, I talked about the REIL translators that turn native assembly code into REIL code. In this fourth part of the series I want to talk about MonoREIL.
MonoREIL is an abstract interpretation framework based on REIL. We have added this framework to BinNavi to help our customers build their own static binary code analysis algorithms. Since MonoREIL provides a standard implementation of an abstract interpretation algorithm, users of MonoREIL only have to implement a few interfaces that define implementation-specific aspects of their custom analysis algorithm.
MonoREIL algorithms operate on so-called instruction graphs. These graphs represent the REIL code you want to analyze. Each node of the graph represents a single REIL instruction. The edges between nodes represent potential control flow transfers between REIL instructions. This graph structure is provided by the MonoREIL framework itself so you do not have to create this graph yourself.
What you have to do is to specify the order in which the instruction graph will be traversed. Some algorithms are easier to implement starting at the entry node of a function and working towards the exit node. Others benefit from starting at the exit node and walking backwards.
If you want to implement an abstract interpretation algorithm yourself, you have to think about the abstract program state you want to model. Imagine you want to track whether a register influences other registers further down the control flow. In this case, your abstract program state would be a set of influenced registers.
In the first step of your algorithm you assign concrete instances of this abstract program state to each node of the instruction graph. These initial program states reflect prior knowledge you already have about the program before the analysis algorithm is run. For the register tracking algorithm you probably do not have any prior knowledge beyond what register you want to track. The instruction graph node where register tracking begins is initialized with the set the contains just the register you want to track. All other nodes are assigned the empty set.
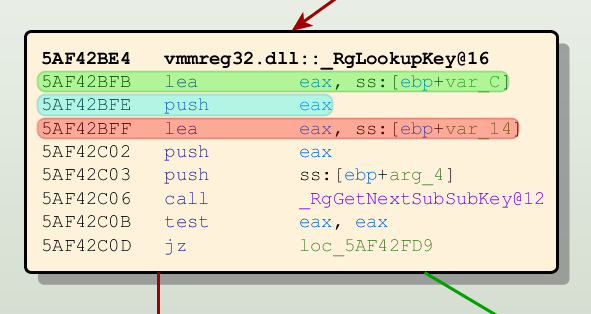
Tracking EAX: Start (green), use (blue), overwritten (red)
Now MonoREIL begins to traverse the graph in the direction you have specified earlier. For each node it encounters on the way, the input abstract program state and the REIL instruction in the node are used to determine the output abstract program state for the node. This transformation is completely dependent on your concrete analysis algorithm and you have to implement the so-called transformation function yourself. For example, if the register tracking algorithm is tracking the register set {eax} and comes across the instruction “add eax, 5, ebx”, the transformation function generates the output set {eax, ebx} because from this instruction on, both the registers eax and ebx depend on eax in some way. If the next instruction is “xor ecx, ecx, eax”, the input set {eax, ebx} is changed to {ebx} because the xor instruction sets eax to a value that does not depend on any of the input registers. After the xor instruction, eax does not depend in any way on the tracked registers and can be removed from the register set.
This is where the reduced instruction set of REIL really begins to shine. Since there are only 17 different instructions, you have to implement at most 17 different transformation functions that turn the input abstract program state of a node into an output abstract program state. In practice, you will have to implement far fewer transformation functions because most algorithms can handle transformations for multiple instructions uniformly (just think about register tracking and the add, sub, mul, div instructions).
The transformation functions are sufficient to do abstract interpretation along a single control flow path. However, they can not be used when multiple control flow paths converge into a single control flow path. To handle this special case, all MonoREIL algorithms have to implement a function that can take an arbitrary number of abstract program states and merge them into a single program state. If the register tracking algorithm receives the set {eax} from one path and the set {ebx} from another path, the input set of the node where these control flow paths merge is the union of the two input sets {eax, ebx}. In the node where the two control flow paths merge, both registers are tainted.
That’s pretty much what you have to do to implement your own code analysis algorithm. There are a few minor implementation details you have to consider to make sure that your MonoREIL algorithm terminates and returns the right result. For example, you have to make sure that your abstract program states never lose previously gained information. If they do, it would be possible to lose information in one step and regain it in the next step, leading to infinite loops where information is constantly lost and regained. This monotonous property of abstract program states is what gave MonoREIL its name.
Once you have defined all of the mentioned interfaces, you can tell MonoREIL to run your analysis algorithm. MonoREIL traverses the instruction graph and applies abstract program state transformations along the control flow path. This process continues until no new information about the program state can be discovered. For each node of the instruction graph, MonoREIL then returns the final abstract program state for the node. This information is the result of the analysis algorithm and can further be interpreted and displayed in the GUI by your custom analysis code.
If you want to know more about MonoREIL you can check out the slides of our CanSecWest 2009 presentation Platform-independent static binary code analysis using a meta-assembly language where we implemented a MonoREIL algorithm to detect array access operations with negative array indices. MonoREIL is also mentioned in the slide sets Applications of the reverse engineering language REIL, Automated static deobfuscation in the context of Reverse Engineering, and The Reverse Engineering Language REIL and its Applications.